Transformata Fouriera: właściwości, zastosowania, przykłady i ćwiczenia
Transformata Fouriera jest metodą adaptacyjnej analizy zorientowanej na funkcje całkowalne, które należą do rodziny transformacji zintegrowanych . Składa się z przedefiniowania funkcji f (t) w kategoriach Cos (t) i Sen (t).
Tożsamości trygonometryczne tych funkcji, wraz z ich charakterystyką derywacji i derywacji, służą do definiowania transformaty Fouriera za pomocą następującej złożonej funkcji:

Jest to prawdą, o ile wyrażenie ma sens, to znaczy gdy niepoprawna całka jest zbieżna. Mówi się algebraicznie, że transformata Fouriera jest homeomorfizmem liniowym.
Każda funkcja, która może pracować z transformatą Fouriera, musi mieć zerowość poza zdefiniowanym parametrem.
Właściwości

Transformata Fouriera spełnia następujące właściwości:
Istnienie
Aby zweryfikować istnienie transformaty Fouriera w funkcji f (t) zdefiniowanej w liczbach rzeczywistych R, muszą zostać spełnione następujące 2 aksjomaty:
- f (t) jest ciągły na kawałki dla wszystkich R
- f (t) jest całkowalny w R
Liniowość transformacji Fouriera
Niech M (t) i N (t) będą dowolnymi dwiema funkcjami ze zdefiniowanymi transformatami Fouriera, ze stałymi a i b, dowolnymi.
F [a M (t) + b N (t)] (z) = a F [M (t)] (z) + b F [N (t)] (z)
Który jest również oparty na liniowości całki o tej samej nazwie.
Transformata Fouriera pochodnej
Mamy funkcję f, która jest ciągła i całkowalna we wszystkich liczbach rzeczywistych, gdzie:

A pochodna f (f ') jest ciągła i definiowana w kawałkach w całym R
Transformata Fouriera pochodnej jest definiowana przez całkowanie przez części za pomocą następującego wyrażenia:
F [f '(t)] (z) = iz F [f (t)] (z)
W pochodnych wyższego rzędu będzie stosowany w sposób homologiczny, gdzie dla wszystkich n 1 musisz:
F [f n '(t)] (z) = (iz) n F [f (t)] (z)
Różnicowanie transformaty Fouriera
Mamy funkcję f, która jest ciągła i całkowalna we wszystkich liczbach rzeczywistych, gdzie:
i (d / dz) F [f (t)] (z) = F [t. f (t)] (z)
Transformacja Fouriera tłumaczenia
Dla wszystkiego θ, które należy do zbioru S i T, który należy do zbioru S ', musi:
F [ τ a θ] = e-iay F [ θ] F [ τ a T ] = e-iax F [ T]
Z τ działa jako operator translacji na wektorze a.
Tłumaczenie transformaty Fouriera
Dla wszystkiego θ, które należy do zbioru S i T, który należy do zbioru S ', musi:
τ a F [θ] = F [e-iax . θ] τ a F [T ] = F [e-iay . T]
Dla wszystkiego, co należy do R
Transformata Fouriera grupy skalowej
Dla wszystkich θ, które należą do zestawu S. T, który należy do zbioru S '
λ należący do R - {0} musisz:
F [θ (λx)] = (1 / | λ |) F [θ] ( y / λ )
F [T (λx)] = (1 / | λ |) F [T] (y / λ )
Jeśli f jest ciągłą i wyraźnie całkowitą funkcją, gdzie a> 0. Następnie:
F [f (at)] (z) = (1 / a) F [f (t)] (z / a)
Aby zademonstrować ten wynik, możesz przejść do zmiany zmiennej.
Gdy T → + następnie s = przy → + ∞
Gdy T → - następnie s = w → - ∞



Symetria
Aby zbadać symetrię transformacji Fouriera, należy zweryfikować tożsamość Parsevala i wzór Plancherela.
Mamy θ i δ, które należą do S. Stąd można wywnioskować, że:

Otrzymywanie
1 / (2π) d { F [θ ], F [δ ] } Tożsamość Parseval
1 / (2π) d / 2 || F [θ ] || Formuła L 2 R d Plancherel
Transformacja Fouriera produktu w splocie
Podążając za podobnymi celami, w transformacie Laplace'a splot funkcji odnosi się do produktu wśród jego transformacji Fouriera.
Mamy f i g jako 2 ograniczone, zdefiniowane iw pełni integrowalne funkcje:
F (f * g) = F (f). F (g)


Następnie podczas zmiany zmiennej
t + s = x; kontynuuje niewłaściwą podwójną całkę



F (f). F (g) = F (f. G)
Ciągłość i upadek w nieskończoności
Dla wszystkiego, co należy do R, F [ θ] spełnia kryteria funkcji ciągłej ograniczonej w Rd.
Również { F [ θ] (y)} → 0 w C, jeśli | y | → ∞
Historia
Ta koncepcja matematyczna została przedstawiona przez Josepha B. Fouriera w 1811 r. Podczas opracowywania traktatu o propagacji ciepła. Został szybko przyjęty przez różne dziedziny nauki i inżynierii.
Został on ustanowiony jako główne narzędzie pracy w badaniu równań różniczkowych cząstkowych, nawet porównując je ze stosunkiem roboczym między transformatą Laplace'a a równaniami różniczkowymi zwyczajnymi.
Do czego służy transformacja Fouriera?
Służy głównie do znacznego uproszczenia równań, podczas przekształcania wyrażeń pochodnych w elementy mocy, które oznaczają wyrażenia różnicowe w postaci całkowalnych wielomianów.
W optymalizacji modulacja i modelowanie wyników działa jak standaryzowane wyrażenie, będące częstym źródłem inżynierii po kilku pokoleniach.
Seria Fouriera
Są one szeregowo zdefiniowane w kategoriach kosinusów i piersi; służą ułatwieniu pracy z ogólnymi funkcjami okresowymi. Po zastosowaniu są one częścią technik rozwiązywania równań różniczkowych cząstkowych i zwykłych.
Szeregi Fouriera są nawet bardziej ogólne niż szereg Taylora, ponieważ rozwijają okresowe funkcje nieciągłe, które nie mają reprezentacji w szeregu Taylora.
Inne formy serii Fouriera
Aby analitycznie zrozumieć transformację Fouriera, ważne jest przejrzenie innych form, w których można znaleźć szereg Fouriera, dopóki nie będziemy mogli zdefiniować szeregu Fouriera w jego złożonej notacji.
- Szereg Fouriera dla funkcji okresu 2L
Wielokrotnie konieczne jest dostosowanie struktury szeregu Fouriera do funkcji okresowych, których okres wynosi p = 2L> 0 w przedziale [-L, L].
- Szereg Fouriera w funkcjach nieparzystych i parzystych
Rozważany jest przedział [-π, π], który oferuje zalety przy korzystaniu z symetrycznych charakterystyk funkcji.
Jeśli f jest równe, szereg Fouriera jest ustalany jako szereg Cosinusów.

Jeśli f jest nieparzyste, szereg Fouriera jest ustalany jako szereg sinusów.

-Kompletna notacja szeregu Fouriera
Jeśli mamy funkcję f (t), która spełnia wszystkie wymagania dla rozwoju szeregu Fouriera, możliwe jest oznaczenie jej w przedziale [-t, t] za pomocą złożonego zapisu:

Aplikacje

Obliczanie podstawowego rozwiązania
Transformata Fouriera jest potężnym narzędziem w badaniu równań różniczkowych cząstkowych typu liniowego ze stałymi współczynnikami. Dotyczą one jednakowo funkcji z domenami nieograniczonymi.
Podobnie jak transformata Laplace'a, transformata Fouriera przekształca funkcję częściowej pochodnej w równanie różniczkowe zwyczajne, które jest znacznie prostsze w obsłudze.
Problem Cauchy'ego dla równania ciepła przedstawia częste pole zastosowania transformaty Fouriera, w którym generowana jest funkcja ciepła rdzenia lub rdzeń Dirichleta.
W odniesieniu do obliczenia podstawowego rozwiązania przedstawiono następujące przypadki, w których często występuje transformacja Fouriera:
- Równanie Laplace'a
- Równanie ciepła
- Równość Schrödingera
- Równanie fal
Teoria sygnału
Ogólny powód zastosowania transformaty Fouriera w tej gałęzi wynika głównie z charakterystycznej dekompozycji sygnału jako nieskończonej superpozycji sygnałów łatwiejszych do leczenia.
Może to być fala dźwiękowa lub fala elektromagnetyczna, transformata Fouriera wyraża ją w superpozycji prostych fal. Ta reprezentacja jest dość częsta w elektrotechnice.
Z drugiej strony istnieją przykłady zastosowania transformaty Fouriera w dziedzinie teorii sygnału:
-Problemy identyfikacji systemu. Ustalony fyg
-Problem z konsekwencją sygnału wyjściowego
-Problemy z filtrowaniem sygnału
Przykłady
Przykład 1
Zdefiniuj transformatę Fouriera dla następującego wyrażenia:

Możemy to również przedstawić w następujący sposób:
F (t) = Sen (t) [H (t + k) - H (t - k) ]
Impuls prostokątny jest zdefiniowany:
p (t) = H (t + k) - H (t - k)
Transformata Fouriera jest stosowana do następującego wyrażenia, które przypomina twierdzenie modulacji.
f (t) = p (t) Sen (t)
Gdzie: F [w] = (1/2) i [p (w + 1) - p (w - 1)]
A transformata Fouriera jest definiowana przez:
F [w] = (1/2) i [(2 / 2w + 1) Sen (k (w + 1)) - (2 / 2w + 1) Sen (k (w-1))]
Przykład 2
Zdefiniuj transformatę Fouriera dla wyrażenia:


Ponieważ f (h) jest funkcją parzystą, można tak powiedzieć


Integracja według części jest stosowana przez wybranie zmiennych i ich różnic w następujący sposób
u = sin (zh) du = z cos (zh) dh
dv = h (eh) 2 v = (eh) 2/2
Zastępowanie masz

Po ocenie pod podstawowym twierdzeniem obliczeń

Stosując wcześniejszą wiedzę na temat równań różniczkowych pierwszego rzędu, wyrażenie jest oznaczone jako

Aby uzyskać K, oceniamy

Wreszcie transformata Fouriera wyrażenia jest zdefiniowana jako

Proponowane ćwiczenia
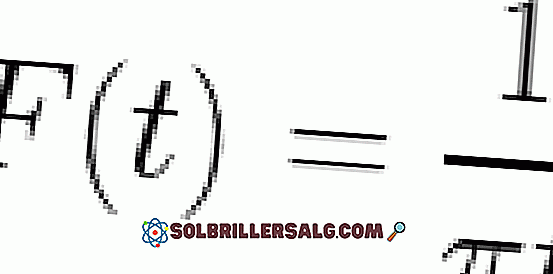

- Uzyskaj transformację wyrażenia W / (1 + w2)









