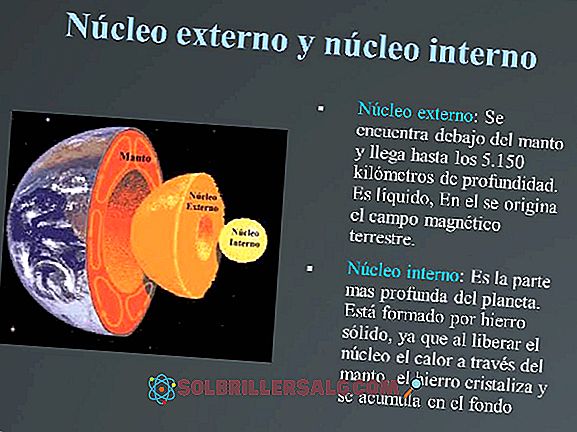
Algebra Boole'a: historia, twierdzenia i postulaty, przykłady
Algebra Boole'a lub algebra Boole'a jest notacją algebraiczną używaną do traktowania zmiennych binarnych. Obejmuje badania każdej zmiennej, która ma tylko 2 możliwe wyniki, komplementarne i wzajemnie się wykluczające. Na przykład zmienne, których jedyną możliwością jest prawda lub fałsz, poprawne lub niepoprawne, włączanie i wyłączanie są podstawą badania algebry Boole'a.
Algebra Boole'a stanowi podstawę cyfrowej elektroniki, co czyni ją dość obecną w czasach współczesnych. Jest on zarządzany przez koncepcję bramek logicznych, na które znacząco wpływają operacje znane w tradycyjnej algebrze.

Historia
Algebra Boole'a została wprowadzona w 1854 r. Przez angielskiego matematyka George'a Boole'a (1815 - 1864), który był wówczas samoukiem. Jego obawa wynikła ze sporu między Augustusem De Morganem a Williamem Hamiltonem o parametry definiujące ten logiczny system.
George Boole argumentował, że definicja wartości liczbowych 0 i 1 odpowiada, w dziedzinie logiki, interpretacji, odpowiednio, Nicości i Wszechświata .
Intencją George'a Boole'a było zdefiniowanie, poprzez właściwości algebry, wyrażeń logiki zdaniowej koniecznej do radzenia sobie ze zmiennymi typu binarnego.
W 1854 roku najbardziej znaczące sekcje algebry Boole'a zostały opublikowane w książce „ Badanie praw myśli, na których opierają się matematyczne teorie logiki i prawdopodobieństwa”.
Ten ciekawy tytuł zostałby podsumowany poniżej jako „ Prawa myśli” („Prawa myśli”). Tytuł przeskoczył do sławy z powodu natychmiastowej uwagi ze strony społeczności matematycznej tamtych czasów.
W 1948 roku Claude Shannon zastosował go w projektowaniu bistabilnych elektrycznych obwodów przełączających. Było to wprowadzenie do zastosowania algebry Boole'a w całym schemacie elektronicznym.
Struktura
Elementarne wartości w tego typu algebrze wynoszą 0 i 1, które odpowiadają odpowiednio FALSE i TRUE. Podstawowe operacje w algebrze Boole'a to 3:
- Operacja AND lub koniunkcja. Reprezentowany przez okres (.). Synonim produktu
- LUB operacja lub rozłączenie. Reprezentowany przez krzyż (+). Synonim sumy.
- Operacja NIE lub negacja. Reprezentowany przez przedrostek NIE (NIE A). Jest również znany jako dodatek.
Jeśli zbiór A definiuje 2 prawa składu wewnętrznego oznaczonego jako iloczyn i suma (. +), To mówi się, że potrójny (A. +) jest algebrą boolowską wtedy i tylko wtedy, gdy wymieniony potrójny spełnia warunek bycia siatką dystrybucyjny
Aby zdefiniować sieć dystrybucyjną, muszą zostać spełnione warunki dystrybucji pomiędzy podanymi operacjami:
, jest dystrybucyjny względem sumy + a. (b + c) = (a. b) + (a. c)
+ jest dystrybucyjny w odniesieniu do produktu. a + (b. c) = (a + b). (a + c)
Elementy składające się na zestaw A muszą być binarne, a więc mieć wartości uniwersalne lub puste.
Aplikacje
Jego głównym scenariuszem zastosowania jest gałąź cyfrowa, która służy do strukturyzacji obwodów, które składają się na operacje logiczne. Sztuka prostoty obwodów na rzecz optymalizacji procesów jest wynikiem prawidłowego stosowania i praktyki algebry Boole'a.
Od rozwoju paneli elektrycznych, poprzez transmisję danych, po programowanie w różnych językach, często możemy znaleźć algebrę boolowską we wszystkich typach aplikacji cyfrowych.
Zmienne boolowskie są bardzo powszechne w strukturze programowania. W zależności od używanego języka programowania będą występować operacje kodu strukturalnego, które używają tych zmiennych. Warunkowe i argumenty każdego języka obsługują zmienne boolowskie w celu zdefiniowania procesów.
Postulaty
Istnieją twierdzenia rządzące strukturalnymi prawami logicznymi algebry Boole'a. Podobnie istnieją postulaty, aby poznać możliwe wyniki w różnych kombinacjach zmiennych binarnych, w zależności od wykonywanej operacji.
Suma (+)
Operator OR, którego elementem logicznym jest związek (U), jest zdefiniowany dla zmiennych binarnych w następujący sposób:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 1
Produkt (.)
Operator AND, którego elementem logicznym jest przecięcie (∩), jest zdefiniowany dla zmiennych binarnych w następujący sposób:
0 0 = 0
0 1 = 0
1 0 = 0
1 1 = 1
Przeciwny (NIE)
Operator NOT, którego elementem logicznym jest uzupełnienie (X) ', jest zdefiniowany dla zmiennych binarnych w następujący sposób:
NIE 0 = 1
NIE 1 = 0
Wiele postulatów różni się od ich odpowiedników w konwencjonalnej algebrze. Wynika to z domeny zmiennych. Na przykład dodanie elementów wszechświata w algebrze Boole'a (1 + 1) nie może dać konwencjonalnego wyniku 2, ponieważ nie należy do elementów zestawu binarnego.
Twierdzenia
Zasada zero i jedność
Każda prosta operacja obejmująca element ze zmiennymi binarnymi jest zdefiniowana:
0 + A = A
1 + A = 1
0 A = 0
1 A = A
Równe uprawnienia lub idempotencia
Operacje między równymi zmiennymi są zdefiniowane jako:
A + A = A
A. A = A
Uzupełnienie
Każda operacja między zmienną a jej dopełnieniem jest definiowana jako:
A + NOT A = 1
A. NIE A = 0
Inwolucja lub podwójne zaprzeczenie
Każda podwójna negacja będzie uważana za zmienną naturalną.
NIE (NIE A) = A
Przemienne
A + B = B + A; Komutatywność sumy.
A. B = B A; Przemienność produktu.
Asocjacyjny
A + (B + C) = (A + B) + C = A + B + C; Łączność sumy.
A. (B. C) = (A. B). C = A B. C; Asocjatywność produktu.
Dystrybucyjny
A + (B. C) = (A + B). (A + C); Dystrybucja sumy względem produktu.
A. (B + C) = (A. B) + (A + C); Dystrybucja produktu w odniesieniu do sumy.
Prawa wchłaniania
Istnieje wiele praw absorpcji między wieloma
A. (A + B) = A
A. (NIE A + B) = A. B
NIE A (A + B) = NIE A. B
(A + B). (A + NIE B) = A
A + A. B = A
A + NOT A. B = A + B
NIE A + A. B = NIE A + B
A. B + A. NIE B = A
Twierdzenie Morgana
Są to prawa transformacji, które obsługują pary zmiennych, które oddziałują między zdefiniowanymi operacjami algebry Boole'a (+.).
NIE (A. B) = NIE A + NIE B
NIE (A + B) = NIE A. NIE B
A + B = NIE (NIE A + NIE B)
A. B = NIE (NIE A. NIE B)
Dwoistość
Wszystkie postulaty i twierdzenia mają zdolność dualności. Oznacza to, że podczas wymiany zmiennych i operacji wynikowa propozycja jest weryfikowana. To znaczy, że przy wymianie 0 na 1 i AND na OR lub odwrotnie; powstaje wyrażenie, które również będzie całkowicie poprawne.
Na przykład, jeśli weźmiesz postulat
1 0 = 0
I stosuje się dualność
0 + 1 = 1
Uzyskuje się kolejny doskonale ważny postulat.
Mapa Karnaugh
Mapa Karnaugha jest diagramem używanym w algebrze Boole'a w celu uproszczenia funkcji logicznych. Składa się z dwuwymiarowego układu podobnego do tablic prawdy logiki zdaniowej. Dane z tabel prawdy można bezpośrednio przechwycić na mapie Karnaugh.
Mapa Karnaugh może pomieścić procesy do 6 zmiennych. W przypadku funkcji o większej liczbie zmiennych zalecane jest użycie oprogramowania w celu uproszczenia procesu.
Zaproponowany w 1953 r. Przez Maurice'a Karnaugh, został ustanowiony jako stałe narzędzie w dziedzinie algebry Boole'a, ponieważ jego implementacja synchronizuje potencjał ludzki z potrzebą uproszczenia wyrażeń boolowskich, kluczowego aspektu płynności procesów cyfrowych.
Przykłady
Algebra Boole'a jest używana do redukcji bramek logicznych w obwodzie, gdzie priorytetem jest doprowadzenie złożoności lub poziomu obwodu do minimalnego możliwego wyrażenia. Wynika to z opóźnienia obliczeniowego, które zakłada każde drzwi.
W poniższym przykładzie będziemy obserwować uproszczenie wyrażenia logicznego do jego minimalnego wyrażenia, używając twierdzeń i postulatów algebry Boole'a.
NIE (AB + A + B). NIE (A + NOT B)
NIE [A (B + 1) + B]. NIE (A + NOT B); Współczynnik A ze wspólnym czynnikiem.
NIE [A (1) + B]. NIE (A + NOT B); Twierdzeniem A + 1 = 1.
NIE (A + B). NIE (A + NOT B); przez Theorem A. 1 = A
(NIE A. NIE B). [NIE A. NIE (NIE B)];
Według twierdzenia Morgana NIE (A + B) = NIE A. NIE B
(NIE A. NIE B). (NIE A. B); Przez podwójne twierdzenie ujemne NIE (NIE A) = A
NIE A. NIE B. NIE A. B; Grupowanie algebraiczne
NIE A. NIE A. NIE B. B; Przemienność produktu A. B = B A
NIE A. NIE B. B; Twierdzeniem A. A = A
NIE A. 0; Twierdzeniem A. NIE A = 0
0; Twierdzeniem A. 0 = 0
A. B. C + NOT A + A. NIE B. C
A. C. (B + NOT B) + NIE A; Faktoring (A. C) ze wspólnym czynnikiem.
A. C. (1) + NIE A; Według twierdzenia A + NOT A = 1
A. C + NOT A; Z reguły zasada zero i jednostka 1. A = A
NIE A + C ; Według prawa Morgana A + NOT A. B = A + B
W tym celu należy rozszerzyć prawo Morgana, aby zdefiniować:
NIE (NIE A). C + NIE A = NIE A + C
Ponieważ NIE (NIE A) = A przez inwolucję.
Uprość funkcję logiczną
NIE A. NIE B. NOT C + NOT A. NIE B. C + NOT A. NIE C do minimalnego wyrażenia
NIE A. NIE B. (NOT C + C) + NIE A. NIE C; Faktoring (NIE A. NIE B) ze wspólnym czynnikiem
NIE A. NIE B. (1) + NIE A. NIE C; Według twierdzenia A + NOT A = 1
(NIE A. NIE B) + (NIE A. NIE C); Z reguły zasada zero i jednostka 1. A = A
NIE A (NIE B + NOT C); Faktoring NIE A ze wspólnym czynnikiem
NIE A. NIE (B. C); Według praw Morgana NIE (A. B) = NIE A + NIE B
NIE [A + (B. C)] Według praw Morgana NIE (A. B) = NIE A + NIE B
Każda z 4 opcji pogrubionych reprezentuje możliwe rozwiązanie obniżenia poziomu obwodu
Uprość funkcję logiczną do minimalnego wyrażenia
(A) NIE B, C + A, NIE B, B, D + NIE A, NIE B). C
(A, NIE B, C + A, 0, D + NIE, NIE B). C; Twierdzeniem A. NIE A = 0
(A, NIE B, C + 0 + NIE A, NIE B). C; Twierdzeniem A. 0 = 0
(A, NIE B, C + NIE A, NIE B). C; Według twierdzenia A + 0 = A
A. NIE B. C. C + NOT A. NIE B. C; Przez dystrybucyjność produktu w odniesieniu do sumy
A. NIE B. C + NOT A. NIE B. C; Twierdzeniem A. A = A
NIE B. C (A + NOT A) ; Faktoring (NIE B. C) ze wspólnym czynnikiem
NIE B. C (1); Według twierdzenia A + NOT A = 1
NIE B. C; Z reguły zasada zero i jednostka 1. A = A